Save you from anything

0%

论文阅读：Inductive Representation Learning on Large Graphs

发表于 更新于 分类于 阅读次数： Valine：

graphSAGE的论文，折腾GCN的人必读一篇论文。GCN计算需要完整图结构，既消耗硬件资源、也没法进行mini-batch学习。

本论文提出了graphSAGE模型，其核心思想是，通过对学习过程进行采样，近似完成GCN的计算过程，从而可以分批采样以达到进行batch学习的目的。另外对于图中新增的节点，只需要对新添加的节点进行采样学习即可。

（这篇论文在2020年1月左右阅读）

研究背景

GCN的一个问题在于，每次学习都需要将整个图送入显存/内存中，资源消耗巨大。另外使用整个图结构进行学习，导致了GCN的学习的固化，图中一旦新增节点，整个图的学习都需要重新进行。这两点对于大数据集和项目实际落地来说，是巨大的阻碍。

graphSAGE的原理

和GCN的论文一样，本咸鱼选择跳过论文中的数学证明，网上有大把比我分析的好的文章，想看数学原理建议阅读论文本体或者去看其他大手子们的文章。我这里只写一些个人理解。

GCN的计算细节

了解了GCN的工作模式之后会发现一个事实，每轮卷积中，每个节点只和自己周围的节点交换信息。如果是单层GCN，那么每个节点只能接受到自己一跳内邻居的信息。两层的话则是两跳（通过一跳邻居间接传播过来），如图所示：

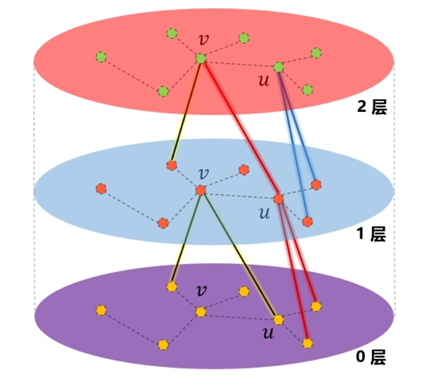
假设我只需要图中一个点的卷积的结果，并且只使用了一层GCN，那么实际上我只需要这个节点和它的全部邻居节点，图中的其他节点是没有意义的；

如果使用了两层GCN，那么我只需要这个节点和它的两跳以内的全部邻居，以此类推。因为更远节点的信息根本无法到达这个节点。

如此，便可以实现GCN的mini-batch，一次取出一组待训练节点和它们训练所需的N跳内的邻居节点即可，因为这些节点的训练本来也不需要更远的节点的信息。

通过采样进行近似

用过抽取出一部分待训练节点和它们的N跳内邻居可以完成这些节点的训练。但并不是说只进行这种操作就可以完成顺利mini-batch训练。例如，图中的某些节点是有几百上千个邻居的超级节点，对于这种节点，哪怕只进行一跳邻居采样，仍然会导致计算困难。

针对这个问题，本论文提出了采样的思路，即，只对目标节点的邻居进行一定数量的采样，然后通过这次被采样出来的节点和目标节点进行计算，从而逼近完全聚合的效果。

graphSAGE的具体实现

有了上述的分析，我们便清楚了graphSAGE的思路是，通过采样实现对整个图进行分批和近似计算。那么就有两个问题需要解决：如何进行采样以及如何进行计算。

采样的实现

作者没有在采样上折腾出花来，而是直接选择了随机采样。原版代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class UniformNeighborSampler(Layer):
    """
    Uniformly samples neighbors.
    Assumes that adj lists are padded with random re-sampling
    """
    def __init__(self, adj_info, **kwargs):
        super(UniformNeighborSampler, self).__init__(**kwargs)
        self.adj_info = adj_info

    def _call(self, inputs):
        ids, num_samples = inputs
        adj_lists = tf.nn.embedding_lookup(self.adj_info, ids) 
        adj_lists = tf.transpose(tf.random_shuffle(tf.transpose(adj_lists)))
        adj_lists = tf.slice(adj_lists, [0,0], [-1, num_samples])
        return adj_lists

可以看到是根据num_samples指定的数量，对邻居进行随机采样。

因为没有什么证据表明，邻居节点的分布遵循某个分布，所以普通的随机采样反而效果较稳定（另外作者可能试过按常见分布的采样方法，改几行代码的事），论文中有关于使用随机采样论证。

前面已经提过，由于GCN的特性：一层GCN中，节点只直接和邻居节点发生信息交换。所以叠加了几层GCN，就应该采样几跳内的邻居节点。

聚合特征的方法

采样完成后，等于是从原图中抽取出来了一个子图。对于这个batch的计算全部在这个子图上完成。

本论文并不是只实现了一个采样，然后计算部分全部照搬GCN（我导师管这种情况叫创新性不够）。而是自己提出了几个聚合信息的方法：

  • 均值聚合：普通均值聚合、基于修正的均值聚合
  • LSTM聚合
  • 池化聚合：均值池化、最大值池化

其中普通均值聚合是简单的将邻居节点取均值，然后和待运算节点连接后，进行一次矩阵变换。

而基于修正的均值聚合的计算公式如下。

这个算法在聚合邻居节点的特征时就已经有了一定的权重，近似模拟GCN的计算过程。

而LSTM聚合是将邻居节点逐个输入LSTM中，因为作者认为LSTM(RNNs)比均值聚合有着更强的特征提取能力。但LSTM是适合于编码顺序数据的，因此每次使用LSTM聚合计算时需要进行一次随机打乱。

而池化聚合是考虑到了GCN的特性，GCN本身就是在平滑同类节点的嵌入结果，而使用均值或最大值池化，更有利于提取同类节点的特征。计算公式如下：

（作者声称，实验结果显示，均值池化和最大值池化没有显著的性能差距，故他们将重点放在了最大值池化上）

实验结果

通常我是不提及实验结果的，因为反正结果做的差也不会发上来。不过这篇论文的结果不是一水的往一个方向倒。所以我把实验结果弄上来。

本论文使用了三个数据集：

  • Web of Science引文数据集。目标是将学术论文分类为不同的主题
  • Reddit帖子。目标是将发帖人归为不同社区的成员
  • 各种生物学蛋白质的功能分类蛋白质-蛋白质相互作用（PPI）图。目标是对未知的PPI图进行概括

实验结果如下：

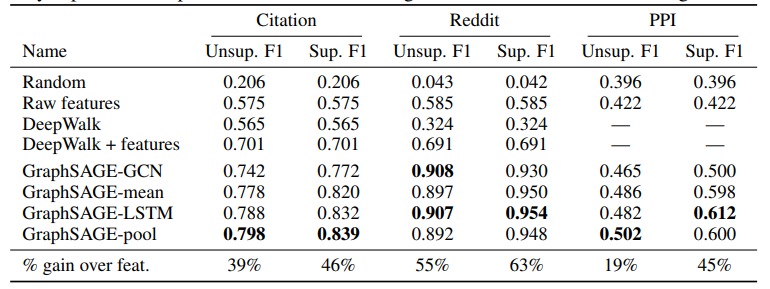
我想说的是：graphSAGE并没有duang的就在三个数据集上都表现出某一个聚合方法比较好。四个方法各有千秋，如果要用graphSAGE建议都试试。

总结

这篇论文也是2017年的了，后面又有一些其他七七八八的针对graph进行采样从而实现mini-batch的算法，某些方面比这篇文章更好，不过这篇文章仍然是GCN项目落地的必读文章之一。